数据清洗 因子分析的主要作用：

1、因子分析特点

因子分析(FA)是一系列用来发现一组变量的潜在结构的方法，通过寻找一组更小　的、潜在的或隐藏的结构来解释已观测到的、变量间的关系。

具有以下特点：

因子的数量远少于原始变量个数，因此因子分析能够减少分析中的工作量。

因子变量不是对原始变量的取舍，而是根据原始变量的信息进行重组，能反映原始变量的大部分信息。

因子之间不存在线性相关关系。

2、因子分析目标

FA的目标是通过发掘隐藏在数据下的一组较少的、更为基本的无法观测的变量，来解释一组可观测变量的相关性。这些虚拟的、无法观测的变量称作因子。（每个因子被认为可解释多个观测变量间共有的方差，也叫作公共因子）

模型的形式为：

Xi=a1F1+a2F2+……apFp+Ui

Xi是第i个可观测变量（i=1,2,……k）

Fj是公共因子（j=1,2,……p）

3、判断需提取的公共因子数

options(digits=2)  #环境变量设置，保留小数2位

covariances<-ability.cov$cov  #计算心理测量数据变量ability的协方差矩阵

correlations<-cov2cor(covariances) #协方差矩阵转换为相关系数矩阵

correlations 

library(psych)  

fa.parallel(correlations,n.obs=112,fa="both",n.iter=100,main="碎石图分析") 

有用的因子分析函数

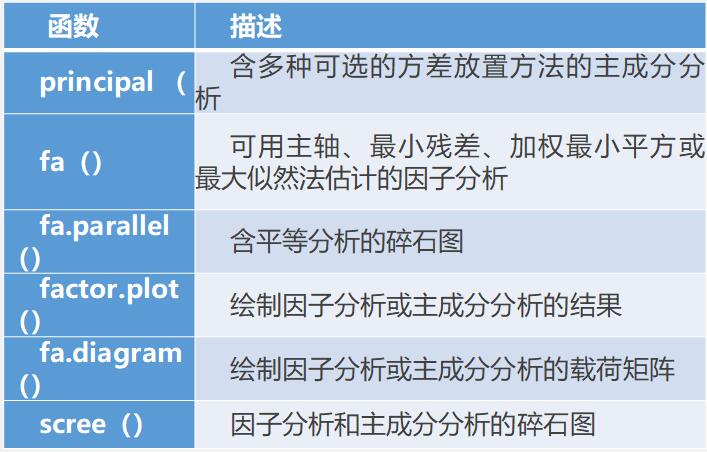
4、因子应用

在市场调研中，研究人员关心的是一些研究指标的集成或者组合，这些概念通常是通过等级评分问题来测量的，如利用李克特量表取得的变量。每一个指标的集合（或一组相关联的指标）就是一个因子，指标概念等级得分就是因子得分。

因子分析在市场调研中有着广泛的应用，主要包括：

消费者习惯和态度研究（U&A）

品牌形象和特性研究

服务质量调查

个性测试

形象调查

市场划分识别

顾客、产品和行为分类

在实际应用中，通过因子得分可以得出不同因子的重要性指标，而管理者则可根据这些指标的重要性来决定首先要解决的市场问题或产品问题。