关联规则的评价标准：

在某些特定情况下，仅凭支持度和置信度来衡量一条规则，是完全不够的，对于数据的筛选力度也不足。因此，需要介绍更多的判断强关联规则的评价标准，来满足实际需求。

支持度和置信度并不能过成功滤掉那些我们不感兴趣的规则，因此我们需要一些新的评价标准，下面介绍六中评价标准：相关性系数，卡方指数，全置信度、最大置信度、Kulc、cosine距离。

1、相关性系数lift

引入正相关和负相关的机制，对于不是正相关的商品规则，可以用相关性系数lift过滤掉。对于规则A->B或者B->A，lift(A,B)=P(A∩B)/(P(A)*P(B))，如果lift(A,B)>1表示A、B呈正相关，lift(A,B)<1表示A、B呈负相关，lift(A,B)=1表示A、B不相关（独立）。实际运用中，正相关和负相关都是我们需要关注的，而独立往往是我们不需要的，两个商品都没有相互影响也就是不是强规则，lift(A,B)等于1的情形也很少，一般只要接近于1，便认为是独立了。

2、卡方系数

卡方分布是数理统计中的一个重要分布，利用卡方系数我们可以确定两个变量是否相关。卡方系数的定义：

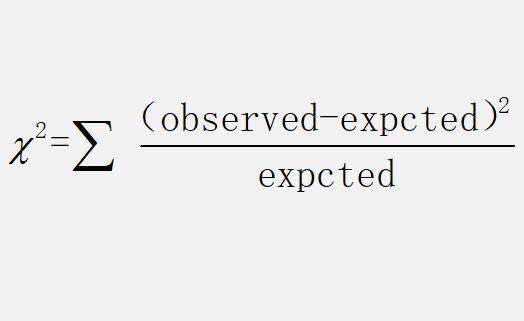
3、全置信度all_confidence

全置信度的定义如下：

all_confidence(A,B)=P(A∩B) / max{P(A),P(B)}=min{P(B|A),P(A|B)}

=min{confidence(A->B),confidence(B->A)}

4、最大置信度max_confidence

最大置信度则与全置信度相反，求的不是最小的支持度而是最大的支持度，max_confidence(A,B) = max{confidence(A->B),confidence(B->A)}，不过感觉最大置信度不太实用。

5、Kulc

Kulc系数本质上是对两个置信度做一个平均处理，公式为：

kulc(A,B)=(confidence(A->B)+confidence(B->A))/2。

6、cosine距离

cosine(A,B)=P(A∩B)/sqrt(P(A)*P(B))=sqrt(P(A|B)*P(B|A))

= sqrt(confidence(A->B)*confidence(B->A))