宽度优先搜索实例：

宽度优先搜索（Breadth First Search，BFS）又称广度优先搜索，是最简便的图的搜索算法之一，这一算法也是很多重要的图的算法的原型。Dijkstra单源最短路径算法和Prim最小生成树算法都采用了和宽度优先搜索类似的思想。

宽度优先搜索（Breadth First Search，BFS）又称广度优先搜索，是最简便的图的搜索算法之一，这一算法也是很多重要的图的算法的原型。Dijkstra单源最短路径算法和Prim最小生成树算法都采用了和宽度优先搜索类似的思想。

所谓广度，就是一层一层的，向下遍历，层层堵截，如对下图3-4进行一次宽度优先遍历的话，我们的结果是：

V_1 V_2 V_3 V_4 V_5 V_6 V_7 V_8

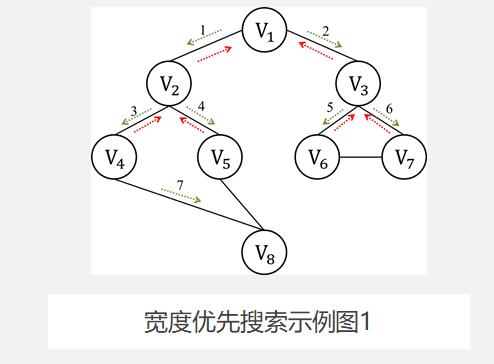
1、访问顶点V_i

2、访问V_i的所有未被访问的邻接点 V_1 , V_2 , … , V_k。

3、依次从这些邻接点（在步骤2中访问的顶点）出发，访问它们的所有未被访问的邻接点，依此类推，直到图中所有访问过的顶点的邻接点都被访问。

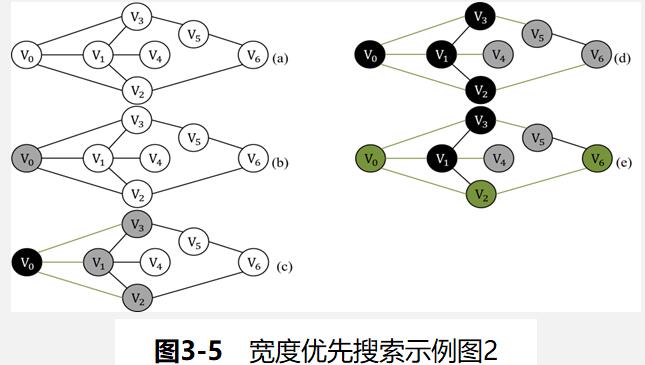
我们采用另一个示例图来说明这个过程，假设我们需要用宽度搜索的方法找到一条从V_0到V_6的最短的路径（一个节点算一步）。

1、在搜索的过程中，初始所有节点是白色（代表了所有点都还没开始搜索），如图3-5(a)所示

2、把起点V_0标志成灰色（表示即将探索V_0），如图3-5(b)所示

3、下一步搜索的时候，我们把所有的灰色节点访问一次，然后将其变成黑色（表示已经被探索过了）。进而再将它们所能到达的节点标志成灰色（因为那些节点是下一步探索的目标点了），但是这里有个判断，当访问到V_1节点的时候，它的下一个节点应该是V_0和V_4，但是V_0已经在前面被染成黑色了，所以不会将它染灰色（即不会回头去探索它），如图3-5(c)所示

4、循环执行步骤3，直到目标节点V_6被染灰色，说明了下一步就到终点了，没必要再搜索（染色）其他节点了，此时可以结束搜索了，整个搜索就结束了，如图3-5(d)所示。然后根据搜索过程，反过来把最短路径找出来，图中把最终路径上的节点标志成绿色，如图3-5(e)所示。