启发式搜索策略的定义和例子：

启发式搜索(Heuristically Search)又称为有信息搜索(Informed Search)，它是利用问题拥有的启发信息来引导搜索，达到减少搜索范围、降低问题复杂度的目的，这种利用启发信息的搜索过程称为启发式搜索。

启发式搜索就是在状态空间中的搜索对每一个搜索的位置进行评估，得到最好的位置，再从这个位置进行搜索直到目标。这样可以省略大量无谓的搜索路径，提高了效率。

   如果能够利用搜索过程所得到的问题自身的一些特征信息来指导搜索过程，则可以缩小搜索范围，提高搜索效率。像这样利用问题自身特征信息来引导搜索过程的方法成为启发式方法。

   启发式策略可以通过指导搜索向最有希望的方向前进，降低了复杂性。通过删除某些状态及其延伸，启发式算法可以消除组合爆炸，并得到令人能接受的解(通常并不一定是最优解)。

然而，启发式策略是极易出错的。在解决问题的过程中启发仅仅是下一步将要采取措施的一个猜想，常常根据经验和直觉来判断。由于启发式搜索只有有限的信息(比如当前状态的描述)，要想预测进一步搜索过程中状态空间的具体行为则很难。一个启发式搜索可能得到一个次优解，也可能一无所获。这是启发式搜索固有的局限性。这种局限性不可能由所谓更好的启发式策略或更有效的搜索算法来消除。

   一般说来，启发信息越强，扩展的无用节点就越少。引入强的启发信息，有可能大大降低搜索工作量，但不能保证找到最小耗散值的解路径(最佳路径)。因此，在实际应用中，最好能引入降低搜索工作量的启发信息而不牺牲找到最佳路径的保证。

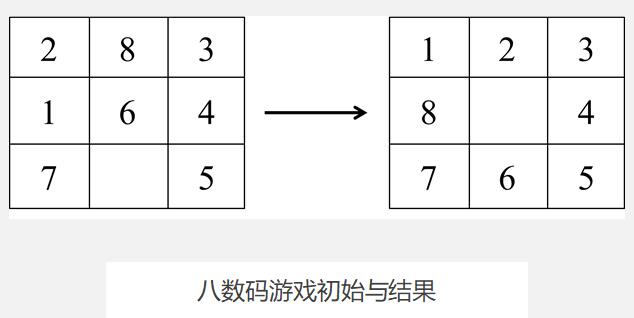
以下为一个启发式搜索的八数码游戏例子：

   如图所示，在一个九宫格里面放入8个数字，数字只能上下左右移动，并且只能移动到空白处。通过若干次这样的移动后，把左图数字位置移动成右图数字位置。

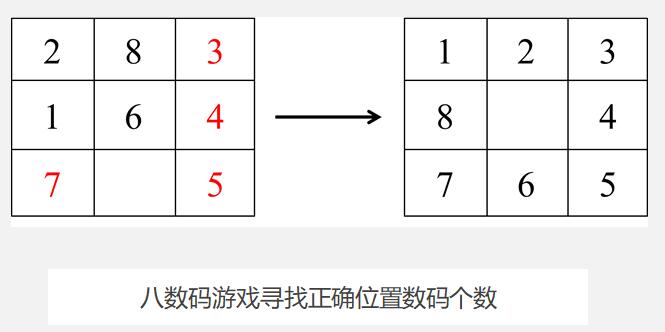
解决此问题的启发策略：每次移动的时候，正确位置数码的个数要大于交换前正确位置数码个数。正确位置数码的个数是指每个数码的位置与最终格局的对比，如果位置相同，则说明此数码在正确位置。图中红色字体标识的数码为正确位置数码，由此我们可以发现下图中左边初始图案正确位置的数码个数为4个。

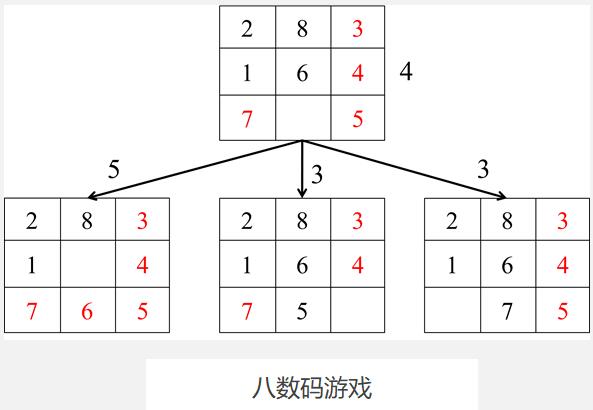
由下图所示可得，正确位置数码个数大于等于4的只有左下方的格局，那么下一步选择的就是左下方的格局。

再次调用次算法如下图所示：

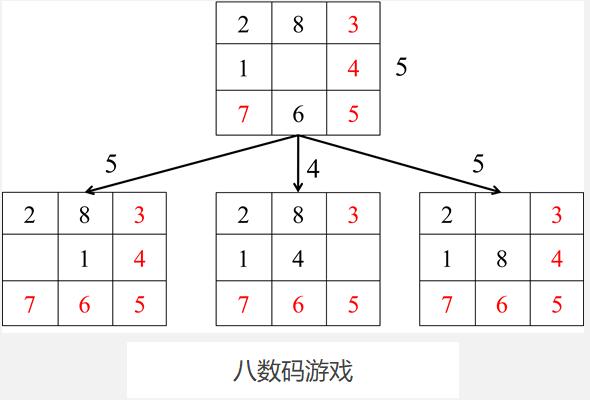
这样一步一步地进行，最终即可得到最终格局。