神经网络模型网络拓扑结构有几种类型：1、前馈型网络。各神经元接收前一层的输入，并输出给下一层，没有反馈。节点分为两类，即输入单元和计算单元，每一计算单元可有任意个输入，但只有一个输出（它可耦合到任意多个其它节点作为其输出）。通常前馈网络可分为不同的层，第i层的输入只与第i-1层输出相连，输入和输出节点与外界相连，而其它中间层则称为隐层。2、反馈型网络所有节点都是计算单元，同时也可接收输入，并向外界输出。

数据建模回归分析是什么意思：回归分析(RegressionAnalysis)是研究变量之间作用关系的一种统计分析方法，其基本组成是一个（或一组）自变量与一个（或一组）因变量。回归分析研究的目的是通过收集到的样本数据用一定的统计方法探讨自变量对因变量的影响关系，即原因对结果的影响程度。回归分析是指对具有高度相关关系的现象，根据其相关的形态，建立一个适当的数学模型(函数式)，来近似地反映变量之间关系的统计分析方法。利用这种方法建立的数学模型称为回归方程，它实际上是相关现象之间不确定、不规则的数量关系的一般化。回归分析分类，如图9.48所示。

自适应选择模型概念：自适应选择模型包含一批模型，如bagging算法，Boosting算法和adaboost算法，它们是一种把若干个分类器整合为一个分类器的方法。首先简要介绍一下bootstrapping方法和bagging方法。1、bootstrapping方法的主要过程主要步骤：重复地从一个样本集合D中采样n个样本。②针对每次采样的子样本集进行统计学习，获得假设Hi。将若干个假设进行组合，形成最终的假设Hfinal。④将最终的假设用于具体的分类任务。2、bagging方法的主要过程主要思路：①训练分类器。从整体样本集合中抽样n*<N个样本，针对抽样的集合训练分类器Ci。②分类器进行投票，最终的结果是分类器投票的优胜结果。

随机森林算法概念：为了克服决策树容易过度拟合的缺点，随机森林算法（RandomForests,RF）在变量（列）的使用和数据（行）的使用上进行随机化，生成很多分类树，再汇总分类树的结果。随机森林在运算量没有显著提高的前提下提高了预测精度，对多元共线性不敏感，可以很好地预测多达几千个解释变量的作用，是当前最好的算法之一。1、随机森林的定义随机森林是一个由决策树分类器集合{h(x,k),k=1,2……}构成的组合分类器模型，其中参数集{k}是独立同分布的随机向量，x是输入向量。当给定输入向量时，每个决策树有一票投票权来选择最优分类结果。每个决策树是由分类回归树（CART）算法构建的未剪枝的决策树。2、随机森林的基本思想随机森林是通过自助法（Bootstrap）重复采样技术，从原始训练样本集N中有放回地重复随机抽取k个样本以生成新的训练集样本集合，然后根据自助样本生成k决策树组成的随机森林。其实质是对决策树算法的一种改进，将多个决策树合并在一起，每棵树的建立依赖一个独立抽取的样本，森林中的每棵树具有相同的分布，分类误差取决于每棵树的分类能力和分类树之间的相关性。

传统决策树模型c4.5算法的基本思想：C4.5算法既可以处理离散型描述属性，也可以处理连续型描述属性。在选择某节点上的分支属性时，对于离散型描述属性，C4.5算法的处理方法与ID3相同，按照该属性本身的取值个数进行计算；对于某个连续性描述属性Ac，假设在某个节点上的数据集的样本数量为total，C4.5算法将做以下处理：将该节点上的所有数据样本按照连续型描述的属性的具体数值，由小到大进行排序，得到属性值的取值序列为{A1c，A2c，……Atotalc}。在取值序列生成total-1个分割点。第i（0<i<total）个分割点的取值设置为Vi=（Aic+A(i+1)c）/2，它可以将该节点上的数据集划分为两个子集。从total-1个分割点中选择最佳分割点。对于每个分割点划分数据集的方式，C4.5算法计算它的信息增益比，并且从中选择信息增益比最大的分割点来划分数据集。

传统决策树模型id3算法基本步骤：1：将训练集S分为1......N个类别。2：计算S的总信息熵INFO(S),改值等于最终类别的各自信息量和概率质量函数的乘积，即每个类别所占训练集的比例乘以该比例的对数值取负，然后加和。3：确定用来进行分类的属性向量V1,V2....Vn4：计算每个属性向量对应的该属性向量对训练集的信息熵INFO(S)Vi，比如对应的属性Vi将训练集分为了M类，那么改值等于在该属性划分下的某一类值出现的概率乘以对应的该值所在的集的信息熵。改值所在的集的信息熵再套公式发现等于最终分类在Vi属性划分下的某一个类里的概率值乘以该概率值的对数值取负。表述的有些复杂，最好看公式。5：在众多属性对于训练集的信息熵之中取最小的，这样信息增益最大。信息增益最大代表着分类越有效。6：完成了一次属性的分裂，之后的递归。

数据建模聚类模型的概念：聚类模型指将物理或抽象对象的集合分组为由类似的对象组成的多个类的分析过程。聚类是一种把两个观测数据根据它们之间的距离计算相似度来分组的方法（没有指导样本）。已经开发了大量的聚类算法，如K-means、Hierachical、Ewkm和BiCluster，操作界面见下图。

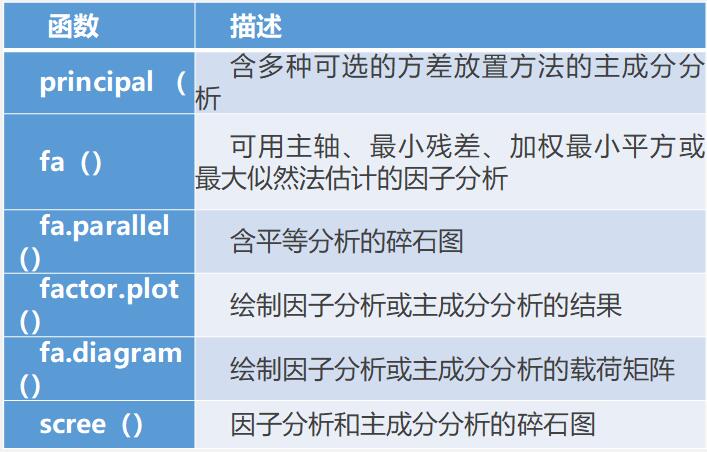
数据清洗因子分析的主要作用：1、因子分析特点因子分析(FA)是一系列用来发现一组变量的潜在结构的方法，通过寻找一组更小的、潜在的或隐藏的结构来解释已观测到的、变量间的关系。具有以下特点：因子的数量远少于原始变量个数，因此因子分析能够减少分析中的工作量。因子变量不是对原始变量的取舍，而是根据原始变量的信息进行重组，能反映原始变量的大部分信息。因子之间不存在线性相关关系。2、因子分析目标FA的目标是通过发掘隐藏在数据下的一组较少的、更为基本的无法观测的变量，来解释一组可观测变量的相关性。这些虚拟的、无法观测的变量称作因子。（每个因子被认为可解释多个观测变量间共有的方差，也叫作公共因子）模型的形式为：Xi=a1F1+a2F2+……apFp+UiXi是第i个可观测变量（i=1,2,……k）Fj是公共因子（j=1,2,……p）3、判断需提取的公共因子数options(digits=2)#环境变量设置，保留小数2位covariances<-ability.cov$cov#计算心理测量数据变量ability的协方差矩阵correlations<-cov2cor(covariances)#协方差矩阵转换为相关系数矩阵correlationslibrary(psych)fa.parallel(correlations,n.obs=112,fa="both",n.iter=100,main="碎石图分析")有用的因子分析函数4、因子应用在市场调研中，研究人员关心的是一些研究指标的集成或者组合，这些概念通常是通过等级评分问题来测量的，如利用李克特量表取得的变量。每一个指标的集合（或一组相关联的指标）就是一个因子，指标概念等级得分就是因子得分。因子分析在市场调研中有着广泛的应用，主要包括：消费者习惯和态度研究（U&A）品牌形象和特性研究服务质量调查个性测试形象调查市场划分识别顾客、产品和行为分类在实际应用中，通过因子得分可以得出不同因子的重要性指标，而管理者则可根据这些指标的重要性来决定首先要解决的市场问题或产品问题。

数据清洗主成分分析法的原理：PCA（PrincipalComponentAnalysis，主成分分析）的思想，就是是一种数据降维技巧，它能将大量相关变量转化为一组很少的不相关变量，这些无关变量称为主成分。PCA的目标是用一组较少的不相关变量代替大量相关变量，同时尽可能保留初始变量的信息，这些推导所得的变量称为主成分，它们是观测变量的线性组合。如第一主成分为：PC1=a1X1=a2X2+……+akXk它是k个观测变量的加权组合，对初始变量集的方差解释性最大。第二主成分是初始变量的线性组合，对方差的解释性排第二，同时与第一主成分正交（不相关）。后面每一个主成分都最大化它对方差的解释程度，同时与之前所有的主成分都正交，但从实用的角度来看，都希望能用较少的主成分来近似全变量集。PCA中需要多少个主成分的准则：根据先验经验和理论知识判断主成分数；根据要解释变量方差的积累值的阈值来判断需要的主成分数；通过检查变量间k*k的相关系数矩阵来判断保留的主成分数。最常见的是基于特征值的方法，每个主成分都与相关系数矩阵的特征值关联，第一主成分与最大的特征值相关联，第二主成分与第二大的特征值相关联，依此类推。利用fa.parallel（）函数，可同时对三种特征值判别准则进行评价。library(psych)fa.parallel(USJudgeRatings[,-1],fa="pc",n.iter=100,show.legend=FALSE,main="碎石图")碎石图、特征值大于1准则和100次模拟的平行分析（虚线）都表明保留一个主成分即可保留数据集的大部分信息principal()函数可根据原始数据矩阵或相关系数矩阵做主成分分析格式为：principal（的，nfactors=,rotate=,scores=）其中：r是相关系数矩阵或原始数据矩阵；nfactors设定主成分数（默认为1）；rotate指定旋转的方式[默认最大方差旋转（varimax）]scores设定是否需要计算主成分得分（默认不需要）。library(psych)(pc<-principal(USJudgeRatings[,-1],nfactors=1))

数据清洗数据集选择标准：1、训练数据集：用于建模；2、验证数据集：用于模型评估，这一过程会导致模型调整，或参数设置，一旦评估的模型满足期待的性能，就可以用于测试集；3、测试数据集：是所谓的外样本集（不可见的观测数据），随机从数据集中选取的观测数据，但在建模中不能使用，重要的是要确保模型是无偏估计。